Introducción
El determinante de una matriz cuadrada es un número que se obtiene a partir de los elementos de la matriz. Su estudio se justifica en cuanto que simplifica la resolución de sistemas lineales y el cálculo de la matriz inversa, entre otras aplicaciones.
En este curso estudiaremos, sobre todo, los determinantes de orden dos y los de orden tres. Los de orden superior se reducirán a éstos.
1.Determinantes de segundo y tercer orden.
Definición 1. Dada una matriz de orden dos 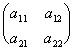 , se llama determinante de la matriz al número que se obtiene así: a11a22 - a12a21.
, se llama determinante de la matriz al número que se obtiene así: a11a22 - a12a21.
Se representa det A ó ½A½.
Ejemplo 1:![]() = 3-(-8) = 11.
= 3-(-8) = 11.
Observación. La interpretación geométrica es que es el área orientada del paralelogramo que determinan los vectores (a11, a12) y (a21, a22).
Se puede ver con detalle en Interpretación Geométrica del determinante, usando el applet Descartes.
Definición 2. Sea A una matriz cuadrada de orden 3, se llama determinante de A al nº que se obtiene así:
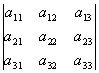 = a11a22a33 + a12a23a31 + a13a21a32 - a13a22a31 - a11a23a32 - a12a21a33.
= a11a22a33 + a12a23a31 + a13a21a32 - a13a22a31 - a11a23a32 - a12a21a33.
Observar que para calcular el determinante se hacen todos los productos posibles de tres elementos que se encuentren en filas y columnas diferentes y luego se suman todos manteniendo el mismo signo o cambiado, según la regla siguiente debida a Sarrus.
Términos positivos Términos negativos
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
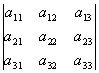
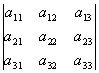
Ejemplo 2. Calcula el valor del determinante de la matriz A =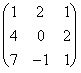 .
.
Aplicando la regla de Sarrus ½A½= 0 + (-4) + 28 - 0 - (-2) -8 = 18
Otra forma práctica de recordar la definición es la siguiente:
Se escriben a la derecha (o debajo) de la matriz las dos primeras líneas. La diagonal principal y sus dos paralelas llevan el signo +, la diagonal secundaria y sus dos paralelas llevan el signo - .
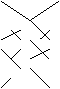 Ejemplo 3. Calcula el valor del determinante
Ejemplo 3. Calcula el valor del determinante  = 16 +15 +18 -10 =39
= 16 +15 +18 -10 =39
2 0 -3
-1 2 1
Ejercicio 1. Calcula los siguientes determinantes:
a) 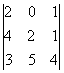 , b)
, b) 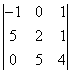 , c) )
, c) ) 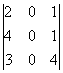 .
.
2. Propiedades de los determinantes
Las propiedades que vamos a enunciar son generales para determinantes de cualquier orden. Pueden comprobarse en los de orden dos o tres.
1. El determinante no varía si se traspone la matriz. Es decir: det A = det At .
(Esta propiedad permite enunciar las demás sólo para filas o columnas).
2. Si permutamos entre sí dos filas (o columnas) el determinante cambia de signo.
3. Si multiplicamos (o dividimos) una fila o columna por un número el determinante queda multiplicado por dicho número.
(Esta propiedad sirve para poder sacar factor común en un determinante)
Ejemplo 4. El determinante  es múltiplo de 5, ya que la primera columna lo es. También es múltiplo de 7, pues lo es la 2ª columna, por lo tanto el determinante es múltiplo de 35..
es múltiplo de 5, ya que la primera columna lo es. También es múltiplo de 7, pues lo es la 2ª columna, por lo tanto el determinante es múltiplo de 35..
Ejercicio 2. Comprueba la afirmación del ejemplo desarrollando por Sarrus.
4. Si todos los elementos de una fila (o columna) son nulos, el determinante también lo es.
5. Si dos filas (o columnas) son iguales (o proporcionales)el determinante es 0.
Ejemplo 5. 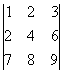 = 0, pues las dos primeras filas son proporcionales.
= 0, pues las dos primeras filas son proporcionales.
6. Si todos los elementos de una línea se descomponen en suma de dos sumandos, el determinante puede descomponerse también como suma de dos determinantes.
Ejemplo 6:
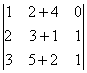 =
= 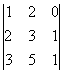 +
+ 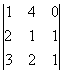 (Comprobarlo)
(Comprobarlo)
7. Si una fila o columna es c.l. de las otras su determinante es cero.
Ejemplo 7. 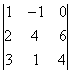 = 0 , pues la 3ª columna es la suma de las dos primeras.
= 0 , pues la 3ª columna es la suma de las dos primeras.
8. Si a una fila (columna) de una matriz se le suma otra fila (columna) multiplicada por un nºel determinante no varía.
Ejemplo 8: A= 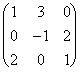 ,a la columna 1ª se le suma la tercera por -2, queda: B=
,a la columna 1ª se le suma la tercera por -2, queda: B=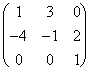 ,
,
![]() = -1 + 12=-11,
= -1 + 12=-11, ![]() = -1-(12) =-11, son iguales.
= -1-(12) =-11, son iguales.
9. Si una matriz cuadrada es triangular (superior o inferior) su determinante es igual al producto de los elementos de su diagonal principal.
Consecuencia: Si I es la matriz identidad su determinante vale 1.
10. El determinante de un producto de matrices (de órdenes iguales) es igual al producto de sus determinantes.
Es decir det AB = det A. det B.
Como consecuencia de esta propiedad:
11. Si $ A-1 entonces ½A½-1 = ![]()
En efecto, A.A-1= I , luego ![]() =
= ![]() = 1, de donde el resultado.
= 1, de donde el resultado.
Ejercicio 3. Indicar las propiedades de los determinantes que permiten escribir las siguientes ecuaciones:
a) ![]() =
=![]() = 8
= 8![]()
b) = 15
= 15 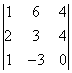 = 15
= 15 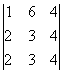
Ejercicio 4. Demostrar[1], sin desarrollar, que son ceros los siguientes determinantes:
a)  ; b)
; b) 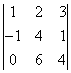 ; c)
; c) 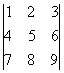 .
.
3. Desarrollo de un determinante por los elementos de una línea.
Definición 1. Si A = (aij) es una matriz cuadrada de orden n, se llama menor complementario del elemento aij, y se representa Mij, al determinante de la submatriz que se obtiene al suprimir de A la fila i y la columna j.
Ejemplo 9. Sea A=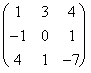 el menor complementario del a21 = -1 es
el menor complementario del a21 = -1 es
M21 = ![]() =-25.
=-25.
Definición 2. Se llama adjunto del elemento aij a: Aij = (-1)i+j Mij.
Nota. El adjunto de un elemento es igual a su menor complementario si la suma de subíndices es par, y a su opuesto si es impar.
Ejemplo 10. El adjunto del elemento a21 = -1, de la matriz de ejemplo 1, es A21=25.
Proposición 1 . Un determinante es igual a la suma de los productos de los elementos de un línea cualquiera por sus respectivos adjuntos.
Demostración.
(La haremos para los de orden 3)
![]() =
=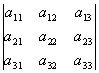 aplicando la regla de Sarrus se tiene:
aplicando la regla de Sarrus se tiene:
½A½= a11a22a33 + a12a23a31 + a13a21a32 - a13a22a31 - a11a23a32 - a12a21a33;
sacando factor común los elementos de la primera fila:
½A½= a11(a22a33-a23a32) + a12(a23a31- a21a33) +a13(a21a32-a22a31), es decir:
½A½= a11 A11 + a12 A12 + a13 A13
Análogamente se haría para cualquier otra línea.
Nota. Esta proposición nos da otra forma de calcular determinantes, se dirá que se ha obtenido su valor desarrollando por los elementos de una línea
Ejemplo 11. Calcula el determinante de A = 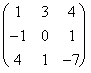
Solución.
Desarrollamos por la 2ª fila:
![]() = - (-1)
= - (-1)![]() + 0 -1
+ 0 -1![]() = -25 + 11 = -14
= -25 + 11 = -14
Proposición 2. La suma de los productos de los elementos de una línea por los adjuntos de otra paralela es cero.
Demostración.
Es inmediata pues correspondería al desarrollo de un determinante con dos líneas iguales, y por las propiedades de los determinantes sería 0.
4. Determinantes de orden cualquiera.
Los métodos que vamos a indicar sirven para determinantes de cualquier orden, aunque nos limitaremos en los ejemplos a los de orden 4 o 5.
M1) Triangulación de un determinante
Utilizando la propiedad 9 de los determinantes podemos conseguir un determinante triangular (sup. o inf. ) y, su valor es el producto de los elementos de la diagonal principal. La técnica para triangular un determinante es similar a la aplicada en el método de Gauss.
Ejercicio 5. Calcula el determinante: D=  , triangulandolo.
, triangulandolo.
M2) Reducción del orden. Se basa en la Proposición 1.
Nota. Como se puede elegir cualquier línea se tomará aquella que tenga más ceros.
Ejemplo 12. Calcula el valor del determinante D=  .
.
Solución: Desarrollando por la 1ª columna:
D = 1.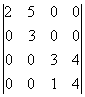 = 1.2.
= 1.2.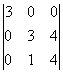 =1.2.3.
=1.2.3.![]() =48
=48
Ejercicio 6. Calcula el valor de D, del ejercicio 1, desarrolllando por la 3ª fila.
Observaciones.
Al calcular un determinante de orden 4, por este método, tenemos que calcular cuatro determinantes de orden tres, que, aunque fácil, es laborioso.
En el ejemplo resuelto resultaba muy “oportuno” el que en las columnas haya tantos 0.
M3) Este método se puede considerar una “combinación” de M1 yM2 .
En primer lugar elegimos una línea y hacemos cero todos sus elementos menos uno; después desarrollamos por dicha línea y así sólo hay que calcular un derterminante de orden tres. Este proceso se puede generalizar.
Ejemplo 13. Calcula el valor de D=  .
.
Solución
Elegimos la fila 3ª vamos a hacer 0 todos los elementos menos el a33,
 C1+ C3 >
C1+ C3 > C2 + 2C3 >
C2 + 2C3 > C4 + 2C3 >
C4 + 2C3 >
 = -
= -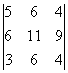 (Terminarle)
(Terminarle)
Determinante de Vandermonde.
El de orden 4 es de la forma V =
Para conseguir ceros en la 1ª columna, se resta, a cada fila la anterior multiplicada por a, empezando desde abajo .
Nos queda: 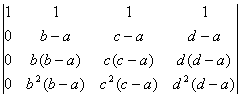 =(b-a)(c-a)(d-a)
=(b-a)(c-a)(d-a)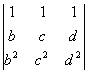
Y da un determinante del mismo tipo pero de orden tres, siguiedo el mismo proceso, 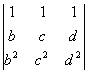 = (c-b)(d-b)
= (c-b)(d-b)![]() = (c-b)(d-b)(d-c).
= (c-b)(d-b)(d-c).
Luego: V = (b-a)(c-a)(d-a)(c-b)(d-b)(d-c).
Ejemplo 14. Calcula el valor de D =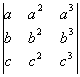 .
.
Solución: Sacando factor común a, b, y c obtenemos
D= a.b.c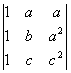 = a.b.c.(b-a)(c-a)(b-c).
= a.b.c.(b-a)(c-a)(b-c).
Pues el determinante que resulta es de Vandermonde.
5. Calculo de la inversa de una matiz cuadrada
Una de las aplicaciones más importantes de los determinantes es que nos da un criterio para decidir cuándo una matriz posee inversa. ![]()
Teorema. Una matriz cuadrada A es inversible Û ½A½¹ 0. Además su inversa es:
A-1 =![]()
 .
.
Demostración .
Es consecuencia inmediata de las proposiciones 1 y 2. (Comprobarlo)
*Este teorema nos da un método para calcular la inversa:
1) Se calcula det A.
Si da 0: A no tiene inversa.
Si da distinto de 0:
2) Se calcula la matriz adjunta de A, adj A, es decir, la que tiene por elementos a los adjuntos de A:
(adj A)= 
3) Se traspone la matriz adjunta. (adj A)t
4) Se divide por el determinante de A.
El resultado es la inversa de A. Es decir :
![]()
| A-1 = |
Ejemplo 15. Calcula la inversa de la matriz A = ![]()
Solución. El determinante de A vale 5, luego tiene inversa.
La matriz adjunta de A es ![]() , su traspuesta es
, su traspuesta es ![]() y A-1=
y A-1= ![]() .
.
Comprobación ![]()
![]() =
=![]() =
=![]()
Ejercicio 7. Calcula la inversa[2], caso de que exista, de la matriz:
A= 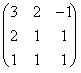
Aplicaciones a la resolución de sistemas lineales
I)Resolución de sistemas lineales por el método de la inversa.
Sea AX =B (1) un sistema de n ecuaciones con n incógnitas.
Si la matriz de los coeficientes, A, tiene un determinante distinto de cero, entonces será inversible, luego multiplicando ambos miembros de (1) por A-1,obtenemos :
A-1 (AX) = A-1B, de donde:.
| X= A-1B |
(2)
II) Regla de Cramer.
Definición. Un sistema con n ecuaciones lineales y n incógnitas se dice que es de Cramer, cuando el determinante de la matriz de los coeficientes es ¹0.
Consecuencia. Todo sistema de Cramer es compatible determinado.
En efecto: S1 AX =B es un sistema de Cramer, entonces existe A-1, luego (2) nos da la solución únia.
Regla de C ramer
Veamos la expresión de las soluciones en el caso de n = 3.
La inversa vimos que es:
A-1 =![]()
 .Þ
.Þ ![]() =
=![]()

![]()
de donde: x =![]() ( b1A11 + b2 A21+ b3 A31)Þ[3]
( b1A11 + b2 A21+ b3 A31)Þ[3]
 .: Análogamente
.: Análogamente

que constituye la llamada regla de Cramer.
Ejemplo 16. Resuelve, usando la regla de Cramer[4], el sistema:
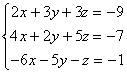
Solución
A = 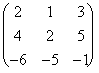 ,
, ![]() = 4 ¹ 0, luego es de Cramer.
= 4 ¹ 0, luego es de Cramer.
x =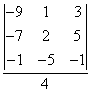 =
= ![]() , y =
, y =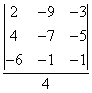 =- = -30, z =
=- = -30, z = 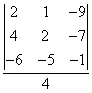 =-11
=-11
Ejemplo 17. Clasifica y resuelve el siguiente sistema según los valores del parámetro k:
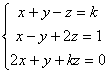
Solución
A= 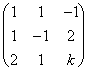 ,
,
![]() = - k - 1 + 4 - 2 - 2 - k = -2k - 1.
= - k - 1 + 4 - 2 - 2 - k = -2k - 1.
Discusión
· Si - 2k -1![]() 0, es decir k
0, es decir k![]() - 1/2, entonces el sistema es de Cramer, luego el sistema es compatible determinado.
- 1/2, entonces el sistema es de Cramer, luego el sistema es compatible determinado.
La solución se encuentra usando la regla de Cramer:
x = 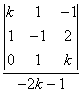 =
= ![]() ,
,
y = 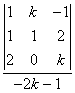 =..... z = ........(acabarle)
=..... z = ........(acabarle)
· Si k = -1/2, el sistema no es de Cramer.
Sustituyendo k por -1/2, obtenemos el sistema:
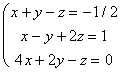
Para clasificarlo y resolverlo usamos Gauss

![]()
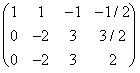
![]()
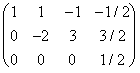 Þ 0z = 1/2
Þ 0z = 1/2
luego el sistema es incompatible.
| Conclusión: Si k distinto de -1/2, compatible determinado; si k=-1/2 incompatible. |
Ejercicio 8. Utiliza la regla de Cramer[5] para resolver el siguiente sistema:
x - y + z = 1
2x +3y -2z = -2
Ejercicio 9. Clasifica y resuelve el siguiente sistema según los valores del parámetro k.
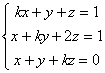
¿Para qué valores de k el sistema es de Cramer? Interpreta geométricamente cada caso.
Problema resuelto[6].
Un sistema económico se divide en tres sectores: 1. Agricultura, 2. Industria y 3. Servicios. Se ha estudiado en un determinado año su economía y se ha obtenido la siguiente tabla Input-Output, en miles de millones de pesetas:
|
| comprador | Demanda | output | |||
|
| 1 | 2 | 3 | final(Di) | total | |
| ven | 1 | 9 | 12 | 0 | 12 | 33 |
| de | 2 | 3 | 31 | 6 | 47 | 87 |
| dor | 3 | 1 | 10 | 5 | 31 | 47 |
|
| Si | 20 | 34 | 36 |
| |
|
| input | 33 | 87 | 47 |
| |
El problema que se plantea es: Si el Gobierno desea que la demanda final suba hasta 16 mil millones para la Agricultura, 85 mil millones para la Industria y 65 mil millones para el sector Servicios, ¿cuáles deben se las salidas (outputs) totales para cada sector.?
Solución:
Repasemos el esquema básico de las técnicas del análisis económico input-output, par el supuesto de una economía con sólo tres sectores.
Si xij representa las ventas (outputs) del sector i al sector j, o lo que es lo mismo las compras (inputs) del sector j al sector i; Dj la demanda final y xj la producción del sector j-ésimo, se puede escribir:
xi1 + xi2 + xi3 + Di = xi ; i = 1,2,3
Estas ecuaciones reflejan la igualdad entre la suma de los importes de las ventas a cada sector productivo y a los consumidores finales (demanda final) con la producción de cada sector.
Llamando aij = xij/xj , (coeficientes técnicos) se verifica que xij = aij xj , con lo que nos quedaría:
ai1 x1 + ai2 x2 + ai3x3 + Di = xi ; i = 1,2,3
Si A= (aij) es la matriz tecnológica6, se puede escribir
A![]() +
+![]() =
=![]() , que puede escribirse: AX + D = X
, que puede escribirse: AX + D = X
Por tanto (I -A)X=D , multiplicando por (I - A)-1 (la inversa de Leontief), sus dos miembros se obtiene:
| X = (I - A)-1D |
igualdad que permite calcular la producción de cada sector conociendo la demanda final.
Apliquemos a nuestros datos estos resultados.
A =  Þ I -A=
Þ I -A=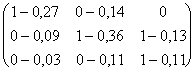 ,
,
Su determinante da 0,393 (comprobarlo) por lo tanto tiene inversa.
Su inversa da:  ,(comprobarlo)
,(comprobarlo)
Luego X = 
![]() »
» ![]()
Ejercicios propuestos del tema
1. Resuelve la siguiente ecuación: 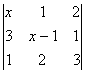 =
=![]()
2. Demuestra que los siguientes determinantes son nulos, sin desarrollarlos.
a)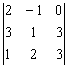 ; b)
; b) 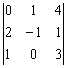 c)
c) 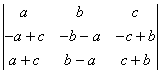
3. Calcula los determinantes ![]() ,
, ![]() y
y ![]() . Aplica los resultados obtenidos para resolver por la regla de Cramer el sistema:
. Aplica los resultados obtenidos para resolver por la regla de Cramer el sistema: ![]()
4. Sea la matriz ![]() . Halla su inversa y calcula A2 – 2A
. Halla su inversa y calcula A2 – 2A
5. Obtener los valores de x, y, z, que verifiquen la siguiente ecuación matricial:
![]() x +
x + 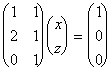
6. Calcula la inversa, caso de que existan, de las matrices siguientes:
a) A = 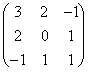 , b) B =
, b) B =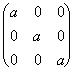 , c) C =
, c) C =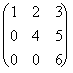 , d) D =
, d) D =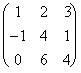

7. Obtener de forma razonada la matriz X que verifica AX = 2B-C
8. ![]()
![]()
![]()
9. Resolver la ecuación matricial XA = B + C, donde
A = 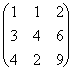 , B =
, B = 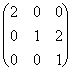 , C =
, C =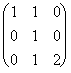
![]()
10. Determinar una matriz cuadrada de orden 2, con determinante igual a -1, de forma que su inversa coincida con su transpuesta.
6. Obtener, en función de a, b y c el valor del determinante:
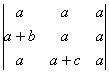
11. Calcula el valor de los determinantes:
a) 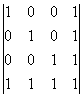 ; b)
; b) 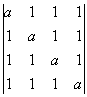
12. Discute el siguiente sistema según los valores del parámetro k:
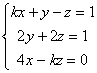
y resuelve en los casos que sea posible.
13. Sabiendo que 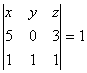 , calcula sin desarrollar:
, calcula sin desarrollar:
a) 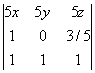 , b)
, b) 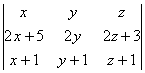
14. Calcula el rango[7] de las matrices:
a) ![]() ; b )
; b )  ;
; 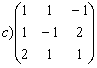 ; d)
; d) ![]()
14. Sea un sistema económico con dos sectores A y B y supongamos que la tabla imput-output es:
|
| Comprador 1 2 | Demanda final | output total | ||
| ven de | 1 | 5 | 3 | 6 | 14 |
| dor | 2
| 4 | 2 | 5 | 11 |
Los datos están en miles de millones de ptas. Si la demanda final pasa a ser de 9 para A y de 4 para B, ¿cuáles deben ser las salidas totales de ambos sectores?
No hay comentarios:
Publicar un comentario